动态规划的介绍

动态规划(Dynamic Programming)，简称DP，是运筹学的一个分支，用于解决多阶段决策过程中的最优化的一种数学方法，把多阶段问题变换为系列单阶段的问题加以解决的方法。

所以动态规划其实是一种数学方法，是求解某类问题的一种方法，不是一种特定的算法，更没有标准的数学表达式或者明确的定义的一种规则。

动态规划的根本是一种解决问题的思路，思考问题的方式，而不是具体的方法。所以动态规划的难点是思想上的，在于如何学会这种思想。这导致如果我们学习不善，很多时候会构造不出来动态规划所需要的形式，甚至根本想不到这是一道动态规划的问题。

而动态规划的基本思想，就是将一个大问题分解成若干个简单的小问题来求解。其中每一个阶段都需要做出决策，从而使得整个过程达到最优。

动态规划的三个重要要素

1. 状态
   动态规划的状态可以相对笼统的理解为“问题所在的局面”，例如，“从第i个数字到第j个数字的最大下降子系列”就是状态，是一种关于i,j的局面，然后“最”大下降子序列就是问题所对应的最优答案。某状态表示的答案（的值），方案（集合），在本质上相同，通常会用一个字母（或）表示。
   状态的答案只依赖状态定义的局面和一些状态以外的常量。在一般情况下，状态变化不会影响状态以外的量，同时状态之后的演变也不受这个状态之前决策的影响。所以在使用动态规划时，应该将所有的可能的变动加入状态的定义中去。
   同时我们也要定义一个初始状态，即初始化，也称为边界条件

2. 状态转移与状态转移方程
   因为要求解最终状态的答案，所以状态之间需要存在某些关系，一般把这种计算关系称作转移，关系式称为状态转移方程。寻找状态转移方程也是求解动态规划问题答案的关键所在。
   状态转移方程一般具有它自己的意义，体现的是从一个状态到另一个状态的变化。对于最优化问题来说，转移方程的目的就是找到最优的前继情况的答案并取出最优答案。
   前继状态的最优解与当前状态之间最优解的关联性被成为动态规划的最优子结构性质。
   对于计数问题来说，转移方程的目的就是不遗漏、不重复地统计所有可能的方案数。
   状态转移存在两种方式，被称为发送型和接收型，前者枚举状态的后继，并计算对后继的贡献;后者枚举状态的前继，当即计算出状态的答案。选取主要取决于前后继状态枚举的难度和转移的复杂程度。

3. 无后效性
   各阶段的决策的一个前提是“仅需要依赖当前状态”，指的是问题的历史状态不影响未来的发展，可以理解为一个局面可以从哪些局面转移过来的单向依赖关系，如果两个局面可以“相互依赖”，即相互转移到达，那么这个问题，或者说你所定义的当前的这个状态，不具备用动态规划解决的性质。
   比如从一道题：一个人从左上角到右下角，其间有各种障碍，问最短路径。当你走到某一个点位的时候，你定义的状态应该是向右或者向下，而不是向左或者向上，因为如果这样，那么该点局面就会转移到上方或者左方，是反向的，形成了所谓的“双向依赖”，这种互相达到是动态规划不可以拥有的。
   我们将这种状态之间不能互相达到的性质以及未来与过去无关的性质统称为动态规划的无后效性。

接下来我们通过例题进行演示

最长字段和

题目描述
给出一个长度为n的序列a,选中期中连续且非空的一段使得这段和最大。

输入格式：
第一行是一个整数n,表示序列的长度；
第二行有n个整数，第i个整数表示。

输出格式：输出一个整数表示答案。

首先需要初始化

对于，有两种方式转移过来

一种是时，我们可以选择枚举到第i个数的最大子段和为第i个数的值加上

一种是时，我们选择枚举到第i个数的自打字段和为

对于这个转移，我们可以进一步思考，如果，那么

同理,如果，那么。

则我们可以写出状态转移方程

还需要一个 维护一个ans为最大值

接下来给出代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 10000007;
int n,f[MAXN],a[MAXN],ans = -1*MAXN;
int main(){
	cin>>n;
	for(int i = 1; i <= n; i++) cin>>a[i];
	for(int i = 1; i <= n; i++) 
	{
		f[i] = max(f[i - 1] + a[i],a[i]);	
		ans = max(ans,f[i]); //维护一个ans为最大值 
	}
	cout<<ans;
	return 0;
}

当然对于此题的状态转移方程，我们也可以写为 这与上式是等价的




接下来我们来看下一道例题

长廊灯泡问题

题目描述
长廊的墙上等距离排列着一列灯泡，每个灯泡发出的亮度不一样，因为灯泡的质量不达标，所以不能出现两个相邻灯泡都打开的情况，否则会因为温度过高导致灯泡毁坏。问灯泡应该怎样开，才可以使长廊的总亮度最大？输出这个最大值。

输入格式：
第一行是一个整数n,表示灯泡的数量；
第二行有n个整数，第i个整数表示灯泡的亮度。

输出格式：输出一个整数表示答案。

初始化

表示第1个灯泡和第2个灯泡只能开一个

接着分析的转移
对于第i个灯泡，有两种情况

1. 如果第i-1个灯泡未开，那么第i个灯泡可以开，即
   
2. 如果第i-1个灯泡打开了，那么第i个灯泡则不能打开，则

我们可以得到状态转移方程

即为最终答案

代码示例如下

1
2
3
4
5
6
7
8
9
10
11
12
13

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 10000007;
int n,f[MAXN],a[MAXN];
int main(){
	cin>>n;
	for(int i = 1; i <= n; i++) cin>>a[i];
	f[1] = a[1];
	f[2] = max(a[1],a[2]);
	for(int i = 1; i <= n; i++) f[i] = max(f[i - 2] + a[i],f[i - 1]);
	cout<<f[n];
	return 0;
}

接着我们给出最后一道例题

[NOIP2002 普及组] 过河卒

题目描述
棋盘上 点有一个过河卒，需要走到目标 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示， 点 、 点 ，同样马的位置坐标是需要给出的。

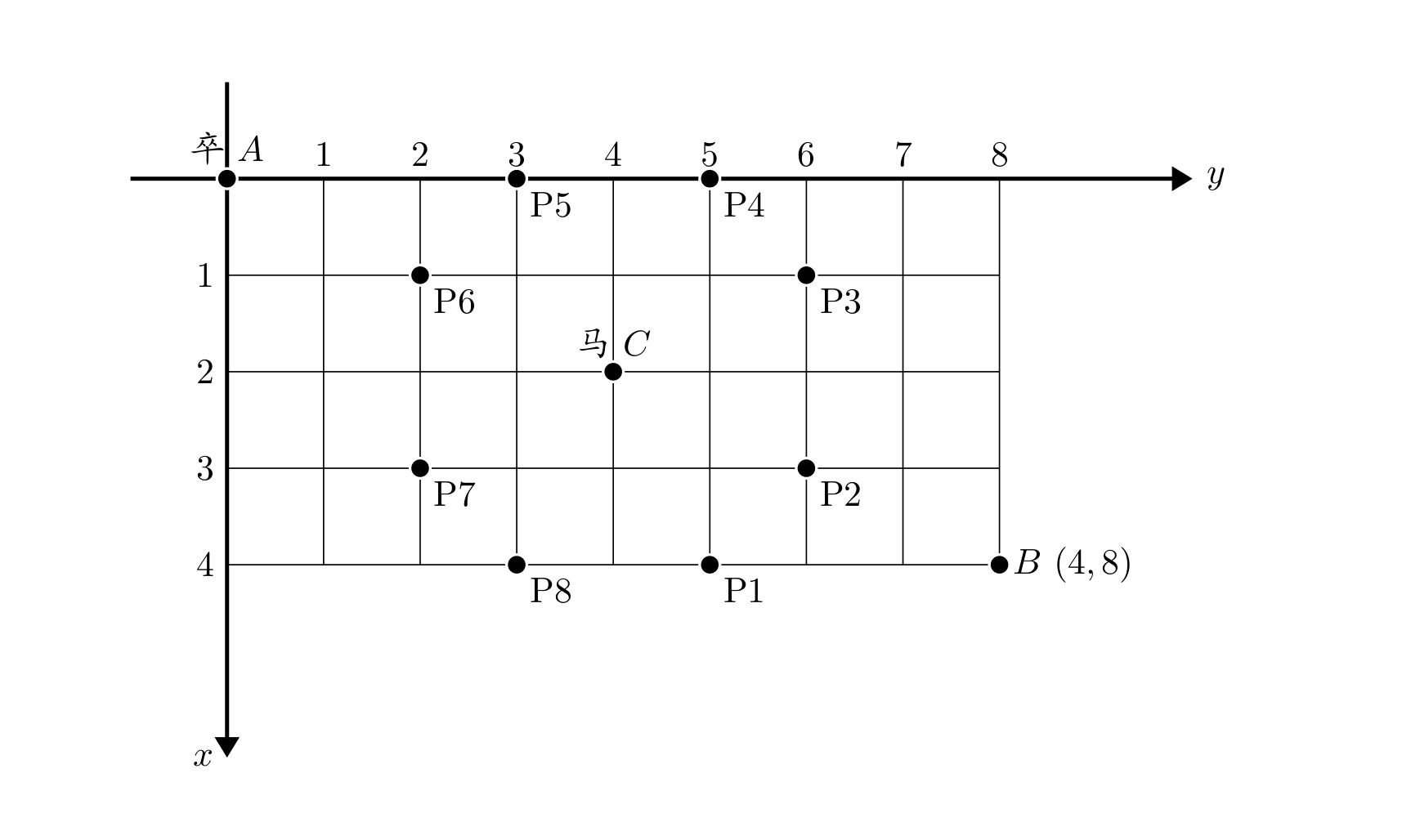
现在要求你计算出卒从 点能够到达 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式
一行四个正整数，分别表示 点坐标和马的坐标。

输出格式
一个整数，表示所有的路径条数。

我们首先分析这道题目，一个点可以由它的上一个点和左边一个点得到，同时也可以由它的右边和下面的点得到。但是dp的一个根本思想是不能形成相互依赖的结构，如果这样，那么便会形成。因为题目是从左上角到右下角，所以一个点的答案只由它左边和上面的点转移而来。是二点方案数的总和。
所以我们的转移方程不难推出

后面给出代码解析

1
2
3
4
5
6
7
8
9

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y;
long long f[50][50]; // 到坐标(i,j)时的方案总数 
//十年oi一场空，不开long long见祖宗 
bool is[50][50]; // 判断是否可以经过 
//数组开大一点 不然跳马可能会越界导致结果出现错误 
int move_x[8] = {1,1,2,2,-1,-1,-2,-2};
int move_y[8] = {2,-2,1,-1,2,-2,1,-1}; //马的八种移动方式对应的坐标的变化 

解释一下 这里需要开long long是因为会出现爆int的情况，这道题也确实卡了int，这在算法题目中需要注意
is数组开大，是因为跳马的落脚点可能超出数组的范围，导致数组越界产生报错。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

cin>>n>>m>>x>>y;
	memset(is,true,sizeof(is)); //默认全部点位可经过 
	memset(f,0,sizeof(f)); //答案默认为0
	is[x][y] = false; //马所在的点为控制点之一，不可经过 
	for(int i = 0; i < 8; i++) is[x + move_x[i]][y + move_y[i]] = false; //八个跳马点标记为不可经过 
	for(int i = 0; i <= n; i++)
	{
		if(!is[i][0]) break;
		f[i][0] = 1;
	}
	for(int j = 0 ; j <= m; j++)
	{
		if(!is[0][j]) break;
		f[0][j] = 1;
	}
	//第0行的都是1，如果有一个点是控制点，那么该点之后的点以及该点都为0 

首先前四行代码不难理解
后面代码的解释：第0行，第0列的所有数的值都应该是1，但是如果期中有一个点是落脚点，那么它无法向后（向下）转移，那么该点之后（包括该点）的所有答案数都应该为0.后面几行代码实现了这样一种落脚点在第0行（列）的特殊情况

接下来给出状态转移的代码

1
2
3

for(int i = 1; i <= n; i++)
	for(int j = 1; j <= m; j++)
		if(is[i][j]) f[i][j] = f[i - 1][j] + f[i][j - 1]; //状态转移方程 

全部代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y;
long long f[50][50];
bool is[50][50];
int move_x[8] = {1,1,2,2,-1,-1,-2,-2};
int move_y[8] = {2,-2,1,-1,2,-2,1,-1}; 
int main(){
	cin>>n>>m>>x>>y;
	memset(is,true,sizeof(is)); 
	memset(f,0,sizeof(f));
	is[x][y] = false;
	for(int i = 0; i < 8; i++) is[x + move_x[i]][y + move_y[i]] = false;
	for(int i = 0; i <= n; i++)
	{
		if(!is[i][0]) break;
		f[i][0] = 1;
	}
	for(int j = 0 ; j <= m; j++)
	{
		if(!is[0][j]) break;
		f[0][j] = 1;
	}
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
			if(is[i][j]) f[i][j] = f[i - 1][j] + f[i][j - 1]; 
	cout<<f[n][m];
	return 0;
}